(一)几何参数计算 

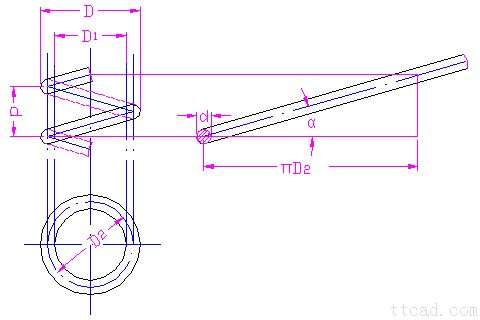
　　普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹 簧丝直径d。由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：

　　式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。　　　　　　　　　　　　　　　　　　

　 

圆柱螺旋弹簧的几何尺寸参数

　　普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表(普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式

参数名称及代号	计算公式		备注
	压缩弹簧	拉伸弹簧
中 径D2	D2=Cd		按普通圆柱螺旋弹簧尺寸系列表取标准值
内 径D1	D1=D2-d
外 径D	D=D2+d
旋绕比C	C=D2/d

压缩弹簧长细比b	b=H0/D2		b在1～5.3的范围内选取
自由高度或长度H0	H0≈pn+(1.5～2)d （两端并紧，磨平） H0≈pn+(3～3.5)d （两端并紧，不磨平）	H0=nd+钩环轴向长度
工作高度或长度 H1,H2,…,Hn	Hn=H0-λn	Hn=H0+λn	λn--工作变形量
有效圈数n	根据要求变形量按式（16-11）计算		n≥2
总圈数n1	n1=n+(2～2.5)（冷卷） n1=n+(1.5～2) （YII型热卷）	n1=n	拉伸弹簧n1尾数为1/4,1/2,3/4整圈。推荐用1/2圈
节 距p	p=(0.28～0.5)D2	p=d
轴向间距δ	δ=p-d
展开长度L	L=πD2n1/cosα	L≈πD2n+钩环展开长度
螺旋角α	α=arctg(p/πD2)		对压缩螺旋弹簧，推荐 α=5°～9°

(

(二)特性曲线 

　　弹簧应具有经久不变的弹性，且不允许产生永久变形。因此在设计弹簧时，务必使其工作应力在弹性极限范围内。在这个范围内工作的压缩弹 簧，当承受轴向载荷P时，弹簧将产生相应的弹性变 形，如右图a所示。为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系(右图b)。 这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。对拉伸弹簧，如图<圆柱螺旋拉伸弹簧的特性曲线> 所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。

　　右图a中的H0是压缩弹簧在没有承受外力时的自由长度。弹簧在安装时，通常预加一个压力 Fmin，使它可靠地稳定在安装位置上。Fmin称为弹簧的最小载荷(安装载荷)。在它的作用下，弹簧的长度 被压缩到H1其压缩变形量为λmin。Fmax为弹簧承受的最大工作载荷。在Fmax作用下，弹簧长度减到H2， 其压缩变形量增到λmax。λmax与λmin的差即为弹簧的 工作行程h,h=λmax-λmin。 Flim为弹簧的极限载荷。在该力的作用下，弹簧丝内的应力达到了材料的弹性极限。与Flim对应的弹簧长度为H3，压缩变形量为λlim。

圆柱螺旋压缩弹簧的特性曲线

　　等节距的圆柱螺旋压缩弹簧的特性曲线为一直线，亦即　　　　　　　　　　　　　　　　 

　　压缩弹簧的最小工作载荷通常取为 Fmin=(0.1～0.5)Fmax；但对有预应力的拉伸弹簧(图<圆柱螺旋拉伸弹簧的特性曲线>)， Fmin>F0，F0为使只有预应力的拉伸弹簧开始变形时所需的初拉力。弹簧的最大工作载荷Fmax，由弹簧在机构中的工作条件决定。但不应到达它的极限载荷，通常应保持Fmax≤0.8Flim。

　　济南弹簧厂的特性曲线应绘在弹簧工作图中，作为检验和试验时的依据之一。此外，在设计弹簧时，利用特性曲线分析受载与变形的关系也较方便。

圆柱螺旋拉伸弹簧的特性曲线